Другие вопросы по: алгебра
Арифм. прогрессия задана формулой cn=93-7n найдите первый отрицательный член прогрессии…
Определите вид треугольника авс, если даны точки а(-1,1), в(7,1), с(3,7)…
Сегодня в школе надо сдать тетрадку по , сидела всю ночь (ибо еще и надо), все решила, но вот не могу справиться с в : с умоляю! кто-нибудь! две машинистки должны были напечата…
1вариант 1.решите уравнение: 3х 5=2х-1 2.в треугольнике авс угол а в 2 раза больше угла в, а угол с в 3 раза больше угла а. вычислите величины углов треугольника авс. 3.решите сис…
Решить урав. х-2под корнем х 3под корнем = 6х-11 все под корнем 7х 1под корнем — 2х 7под корнем = 3х-18 все под корнем…
(x-1)^3 — (x 1)^3 меньше или равно x-6x^2…
Огэ 2020 прототипы заданий 1-5 (плодоовощное хозяйство) — математическая шкатулка
Прочитайте внимательно текст и выполните задания 1 — 5.
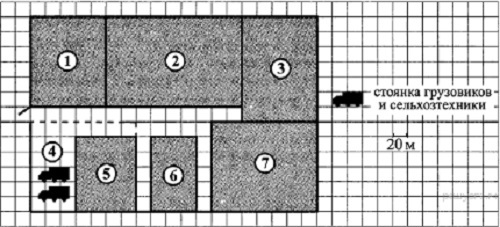
На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы (сторона каждой клетки на плане равна 20 м). Въезд и выезд осуществляются через единственные ворота.
При входе на территорию хозяйства слева от ворот находится кукурузное поле. Рядом с ним расположен яблоневый сад. Также имеется цех по переработке овощей и фруктов, расположенный рядом с полем, засеянным капустой. При входе справа от ворот находится стоянка для грузовиков и сельхозтехники. На территории стоянки расположен склад готовой продукции. Участок с теплицами, в которых выращивают клубнику, граничит с яблоневым садом и капустным полем. К хозяйству подведено электричество.
Задание 1 (ОГЭ 2020)
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Решение:
Рассмотрев план и проанализировав текст, можно записать, что яблоневый сад на плане соответствует цифре 2. В задаче сказано, что теплицы с клубникой граничат с капустным полем и яблоневым садомЮ то есть расположены между ними. Значит, теплицы с клубникой — 3, а капустное поле — 7. Цех по переработке овощей и фруктов граничит с капустным полем. На схеме цех обозначен цифрой 6.
Ответ: 2763.
Задание 2 (ОГЭ 2020)

Решение: 1 га = 10 000 м2. Найдем площадь кукурузного поля. Это площадь прямоугольника со сторонами 5х20 м и 6х20 м, то есть 100 м и 120 м. Площадь поля равна 120 * 100 = 12 000 м2 = 12 га.
Найдем урожайность кукурузы на данном участке.
12 * 4 т = 48 т = 48 * 1000 кг = 48 000 кг = 48 000 * 1000 г = 48 000 000 г.
Подсчитаем какое максимальное количество банок выпустит перерабытывающий цех данного хозяйства.
48 000 000 : 280 = 17142(остаток 24 г).
Ответ: 17142 банки с кукурузой выпустит цех.
Задание 3 (ОГЭ 2020)
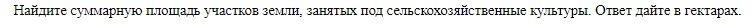
Решение: Найдем площади всех участков под сельхозкультуре на плане.
S = 5 * 6 5 * 7 6 * 7 9 * 6 = 30 35 42 54 = 161.
Площадь каждой клетки на местности составляет: 20 * 20 = 400 м2 .
Итак, площадь под сельхозкультуры равна 161 * 400 м2 = 64 400 м2 .
Учитывая, что 1 га = 10 000 м2 , имеем: 64 400 м2 = 6,44 га.
Ответ: 6,44.
Задание 4 (ОГЭ 2020)
По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).
Решение: Найдем периметр кукурузного поля.
P = 2(5 6) * 20 м = 22 * 20 м = 440 м.
Ответ: 440.
Задание 5 (ОГЭ 2020)
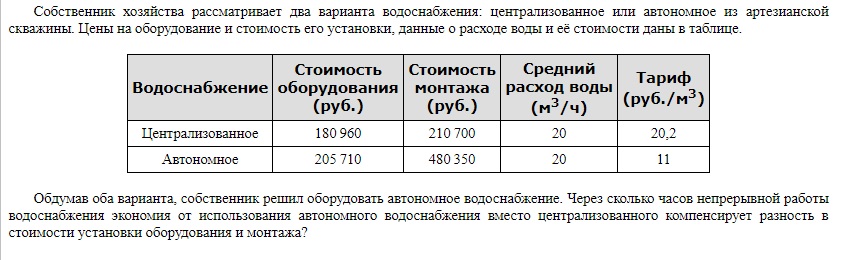
Решение:
- Найдем разность в стоимости оборудования и установки двух вариантов водоснабжения. (205710 480350) — (180960 2107100 = 294400 (рублей).
- 20 * 20,2 руб. = 404 руб. — стоимость часа работы центрального водоснабжения.
- 20 * 11 руб. = 220 руб. — цена часа работы автономного водоснабжения.
- 404 — 220 = 184 (руб.) — экономия от использования автономного водоснабжения.
- 294400 : 184 = 1600 (часов) — компенсируется разность в стоимости оборудования и установки.
Ответ: 1600.
ПЕРСПЕКТИВНАЯ МОДЕЛЬ ОГЭ ПО МАТЕМАТИКЕ 2020 РЕШЕНИЕ ЗАДАНИЙ 1 — 5
Популярные вопросы
.(Найдите объем прямоугольного параллелепипеда, сли его измерения 48дм,16 дм и 12 дм)….
.(Вокруг пруда квадратной формы русалкам нужно посадить 14 ив чтобы вдоль каждого берега росло одинаковое количество деревьев. как это сделать?)….
1)sin^2x-sin^2x=0 2)6sin^2x 4sinxcosx=1…
В17 ч 45 мин из дома одновременно вышли коля и серёжа и пошли в одном направлении. в какое время расстояние между ними стало равным 300 м, если коля двигался со скоростью 80 м/мин,…
Решите уравнения (x 2)² 9(x 2) 20=0. (x-5)² 2(x-5)-63=0….
При окислении 13,8 г этанола оксидом меди(2) получили 9,24 г альдегида. определите выход продукта реакции в процентах…
Найти область определения функции 1) у= 3/ 2x 1 2) y= корень из 16-х в квадрате…
Сочинени на тему ‘смех’ в комедии «ревизор».напишите…
Сдвух ульев за год получили 78 кг меда. с одного из них получили 43кг. на сколько килограммов меда получили больше с одного улья, чем с другого?…
Вкиоске было 39 роз. саша купил 1/3 всех роз, а володя на 4 розы меньше, чем саша. сколько роз осталось в киоске?…
Решение.
Найдём периметр детской площадки:
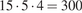 м.
м.
Решу огэ
Сделаем построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём
Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть
Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда
Аналогично из равенства треугольников COM и COK получаем
а из равенства треугольников BOL и BOM —
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
Площадь параллелограмма равна произведению высоты на основание:
Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма:
Площадь параллелограмма равна:
Ответ:
Приведем другое решение.
Сделаем построения и введём обозначения, как показано на рисунке. Пусть O— центр окружности, вписанной в треугольник ABC, точки K, K, M — точки касания окружности со сторонами AC,AB и BC соответственно.
Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
Из прямоугольного треугольника AOH найдем AH:
Следовательно, треугольники AOK и AOH равны по трем сторонам, тогда ∠OAK = ∠AOH.
Центр вписанной окружности лежит на пересечении биссектрис треугольника, следовательно, AO — биссектриса, тогда ∠BAO = ∠OAK = ∠AOH. Углы BAO и AOH — накрестлежащие при пересечении прямых AB и OH секущей AO, следовательно, прямые AB и OH параллельны, значит, ABCD — прямоугольник.
Пусть r — радиус окружности, вписанной в треугольник ABC, r = OK = 3.
В прямоугольном треугольнике ABCAL = AK = 4, LB = BM = r = 3, MC = CK по свойству касательных. Пусть MC = CK = x. Тогда по теореме Пифагора
Следовательно, стороны прямоугольника ABC: AB = 4 3 = 7, BC = 3 21 = 24, тогда его площадь
§
Проведём построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник
Центр вписанной окружности — это точка пересечения биссектрис, поэтому
— биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём
Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть
Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда
Аналогично из равенства треугольников COM и COK получаем
а из равенства треугольников BOL и BOM —
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
Площадь параллелограмма равна произведению высоты на основание:
Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма:
Площадь параллелограмма равна:
Ответ:
§
Сделаем построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём
Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть
Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда
Аналогично из равенства треугольников COM и COK получаем
а из равенства треугольников BOL и BOM —
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
Площадь параллелограмма равна произведению высоты на основание:
Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма:
Площадь параллелограмма равна:
Ответ:
Приведем другое решение.
Сделаем построения и введём обозначения, как показано на рисунке. Пусть O— центр окружности, вписанной в треугольник ABC, точки K, K, M — точки касания окружности со сторонами AC,AB и BC соответственно.
Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
Из прямоугольного треугольника AOH найдем AH:
Следовательно, треугольники AOK и AOH равны по трем сторонам, тогда ∠OAK = ∠AOH.
Центр вписанной окружности лежит на пересечении биссектрис треугольника, следовательно, AO — биссектриса, тогда ∠BAO = ∠OAK = ∠AOH. Углы BAO и AOH — накрестлежащие при пересечении прямых AB и OH секущей AO, следовательно, прямые AB и OH параллельны, значит, ABCD — прямоугольник.
Пусть r — радиус окружности, вписанной в треугольник ABC, r = OK = 3.
В прямоугольном треугольнике ABCAL = AK = 4, LB = BM = r = 3, MC = CK по свойству касательных. Пусть MC = CK = x. Тогда по теореме Пифагора
Следовательно, стороны прямоугольника ABC: AB = 4 3 = 7, BC = 3 21 = 24, тогда его площадь









